Forecasting with Trees Using Darts

Darts provides wrappers for tree-based models. In this section, we benchmark random forest and gradient-boosting decison tree (GBDT) on the famous air passenger dataset. Through the benchmarks, we will see the key advantage and disadvantage of tree-based models in forecasting.

Just Run It

The notebooks created to produce the results in this section can be found here for random forest and here for gbdt .

The Simple Random Forest

We will build different models to demonstrate the strength and weakness of random forest models. The focus will be in-sample and out-of-sample predictions. We know that trees are not quite good at extrapolating into realms where the out-of-sample distribution is different from the training data, due to the constant values assigned on each leaf. Time series forecasting in real world are often non-stationary and heteroscedastic, which implies that the distribution during test phase may be different from the distribution of the training data.

Data

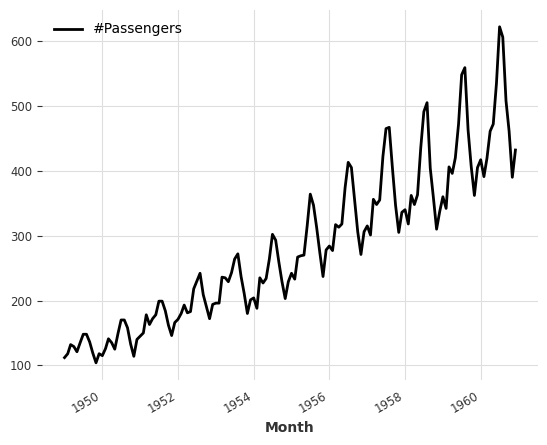
We choose the famous air passenger data. The dataset shows the number of air passengers in each month.

Baseline Model: "Simply Wrap the Model on the Data"

A naive idea is to simply wrap a tree-based model on the data. Here is choose RandomForest from scikit-learn.

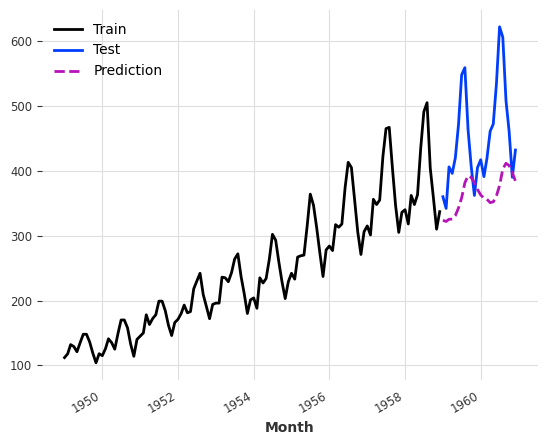
The predictions are quite off. However, if we look into the in-sample predictions, i.e., time range that the model has already seen during training, we would not have observed such bad predictions.

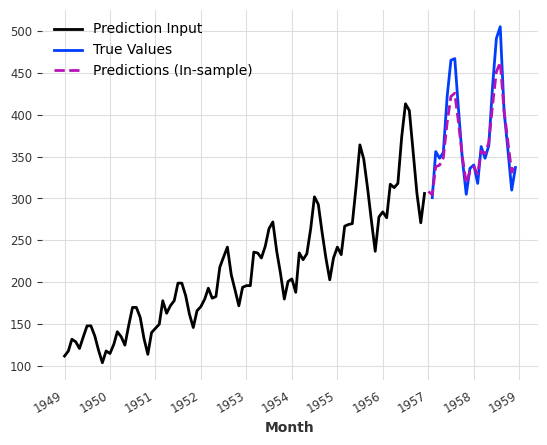
This indicates that there are some new patterns in the data to be forecasted. That is the distribution of the data is different, i.e., the level of the values is higher than before, and the variance is also higher. This is a typical case where trees are not good. However, trees can handle such cases if we preprocess the data to bring the data to the same level and also reduce the changes in variance.

Detrend but also a Clairvoyant Model

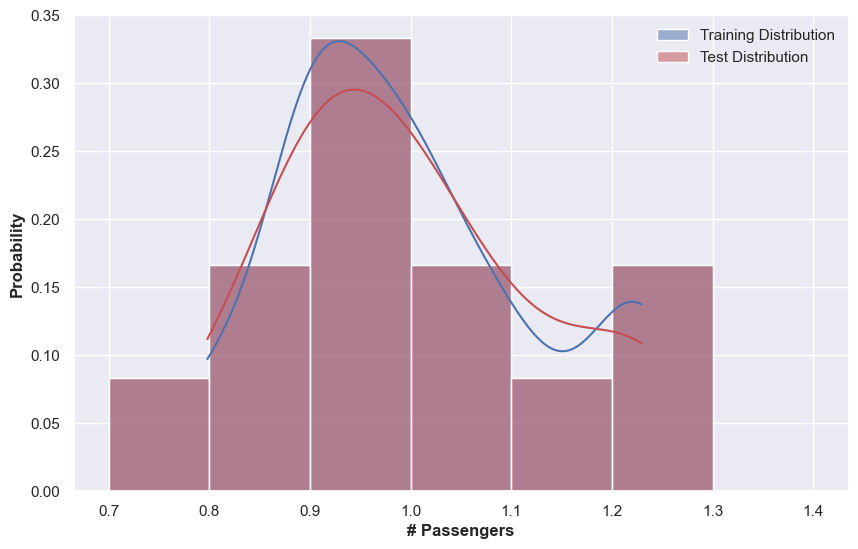
To confirm that this is due to the mismatch of the in-sample distribution and the out-of-sample distribution, we plot out the histograms of the training series and the test series.

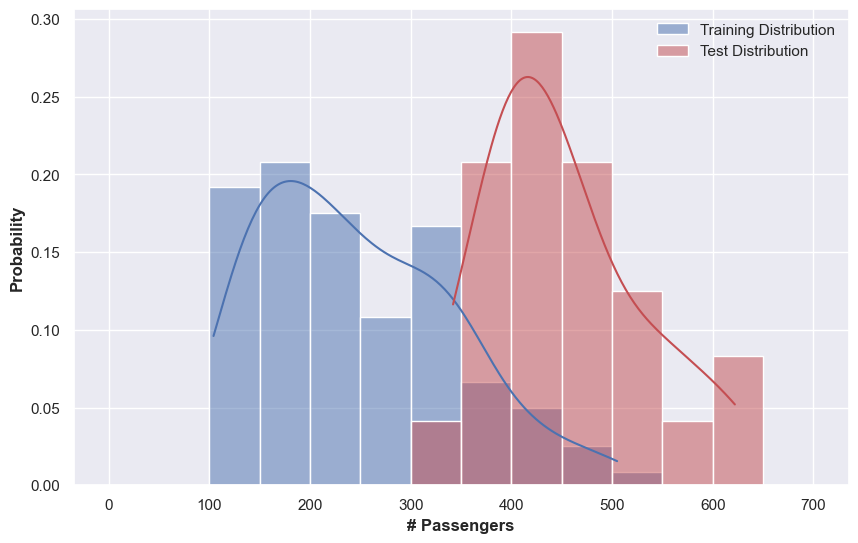
This hints that we should at least detrend the data. In this example, we use a simple moving average while assuming multiplicative components to detrend the data. The detrended data is shown below. Without even training the model, we immediately see that forecasting for such simple patterns is easier than the patterns in the raw data.

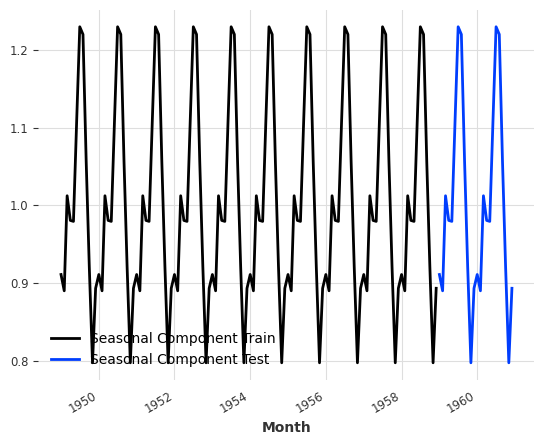
To illustrate that detrending helps, we will cheat a bit to detrend the whole series to confirm that the forecasts are better.

Distribution of Detrended Data

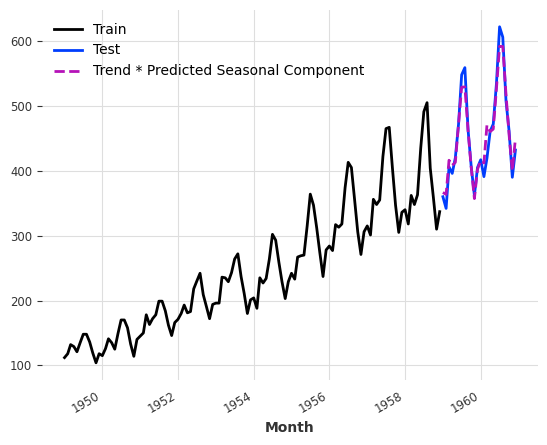
A Formal Model to Use Detrending and without Information Leak

The above method leads to a great result, however, with information leakage during the detrending. Nevertheless, this indicates the performance of trees on out-of-sample predictions if we only predict on the cycle part of the series. In a real-world case, however, we have to predict the trend accurately for this to work. To better reconstruct the trend, we use Box-Cox transformations to stablize the variance first. The following plot shows the transformed data.

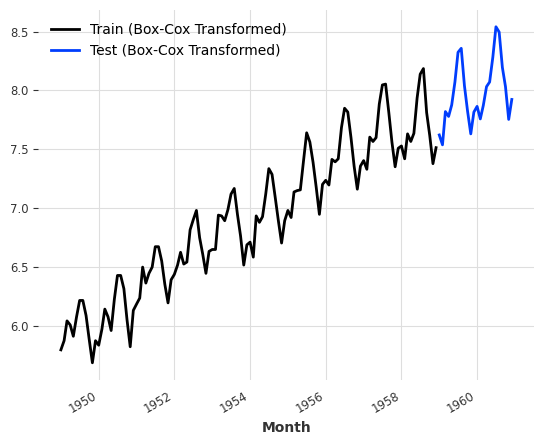
With the transformed data, we build a simple linear trend using the training dataset and extrapolate the trend to the dates of the prediction.

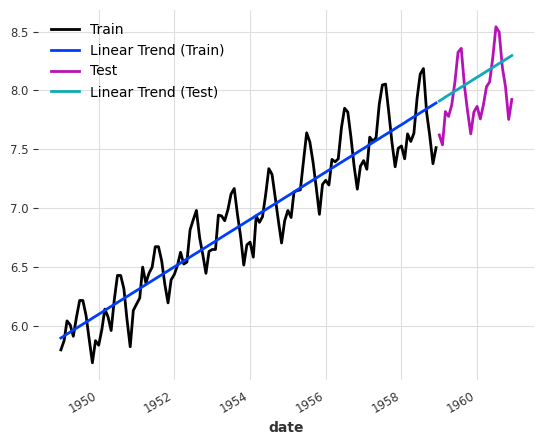
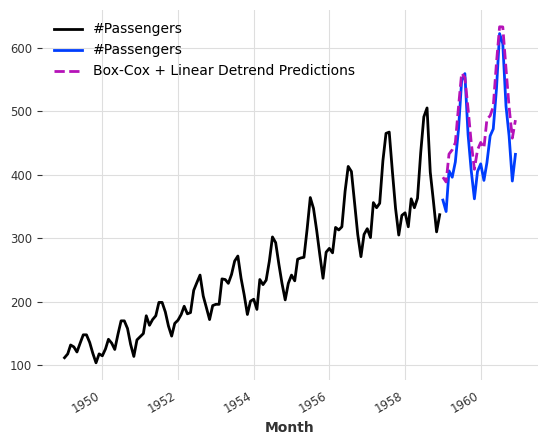
Finally, we fit a random forest model on the detrended data, i.e., Box-Cox transformed data - linear trend, then reconstruct the predictions, i.e., predictions + linear trend + Inverse Box-Cox transformation. We observed a much better performance than the first RF we built.

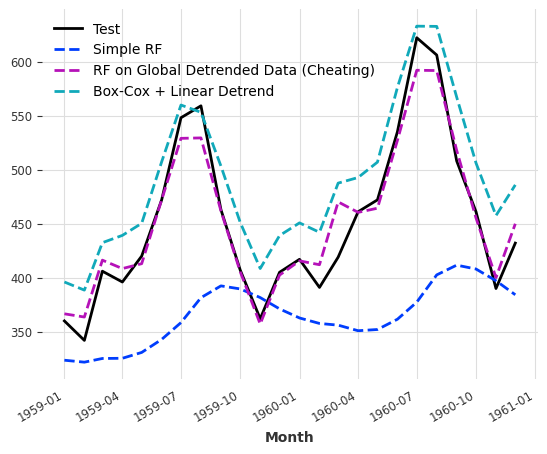
Comparisons of the Three Random Forest Models

Observations by eyes showed that cheating leads to the best result, followed by a simple linear detrend model.

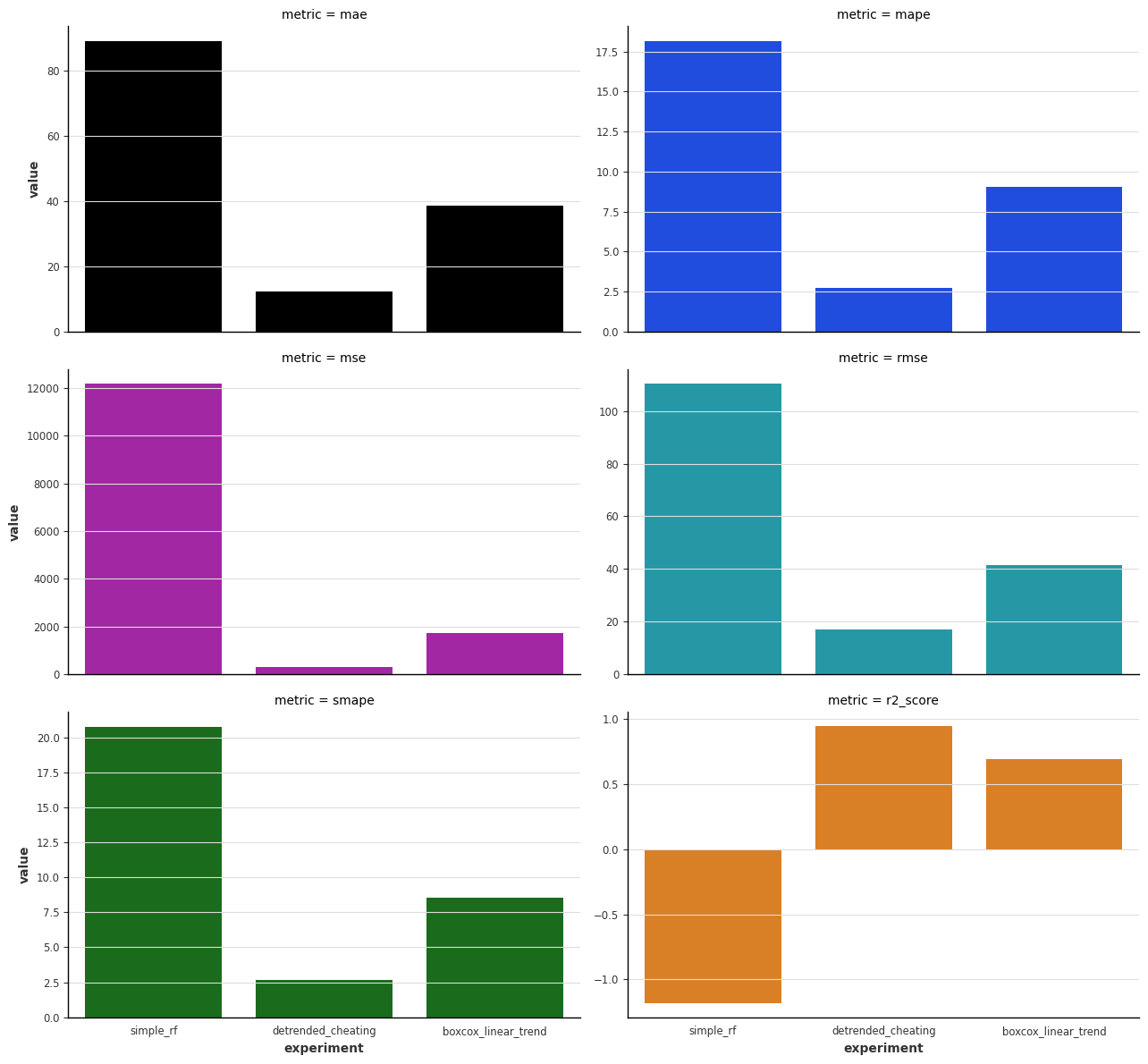
To formally benchmark the results, we computed several metrics. For most of the metrics, the detrend (cheating) model is the best, which is expected since it is a clairvoyant model peeks into the future. The second best is the box-cox + linear trend model.

Gradient Boosted Trees

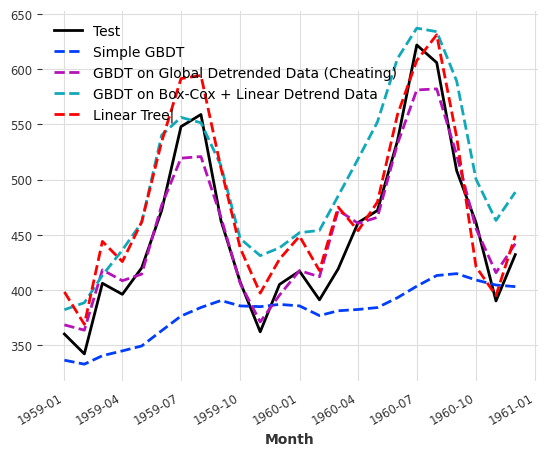
Similar behavior is also observed for gradient-boosted decision trees (GBDT). We perform exactly the same steps as we did for random forest model. The results are shown below. For GBDT, we also tested the linear tree model too².

Why Linear Tree

For trees, the predictions are flat lines within a bucket of values. For example, we may get the same prediction for a given feature value 10 and 10.1 as the two values are so close to each other. However, without detrending, we expect the predictions to have a uplift trend in our data.

To count for this, LightGBM has a parameter called linear_tree². This parameter allows the model to fit a linear model on the leaf nodes to capture the trend. This means that we do not need to detrend the data before fitting the model. In this specific example, we see that the linear tree model performs quite well.

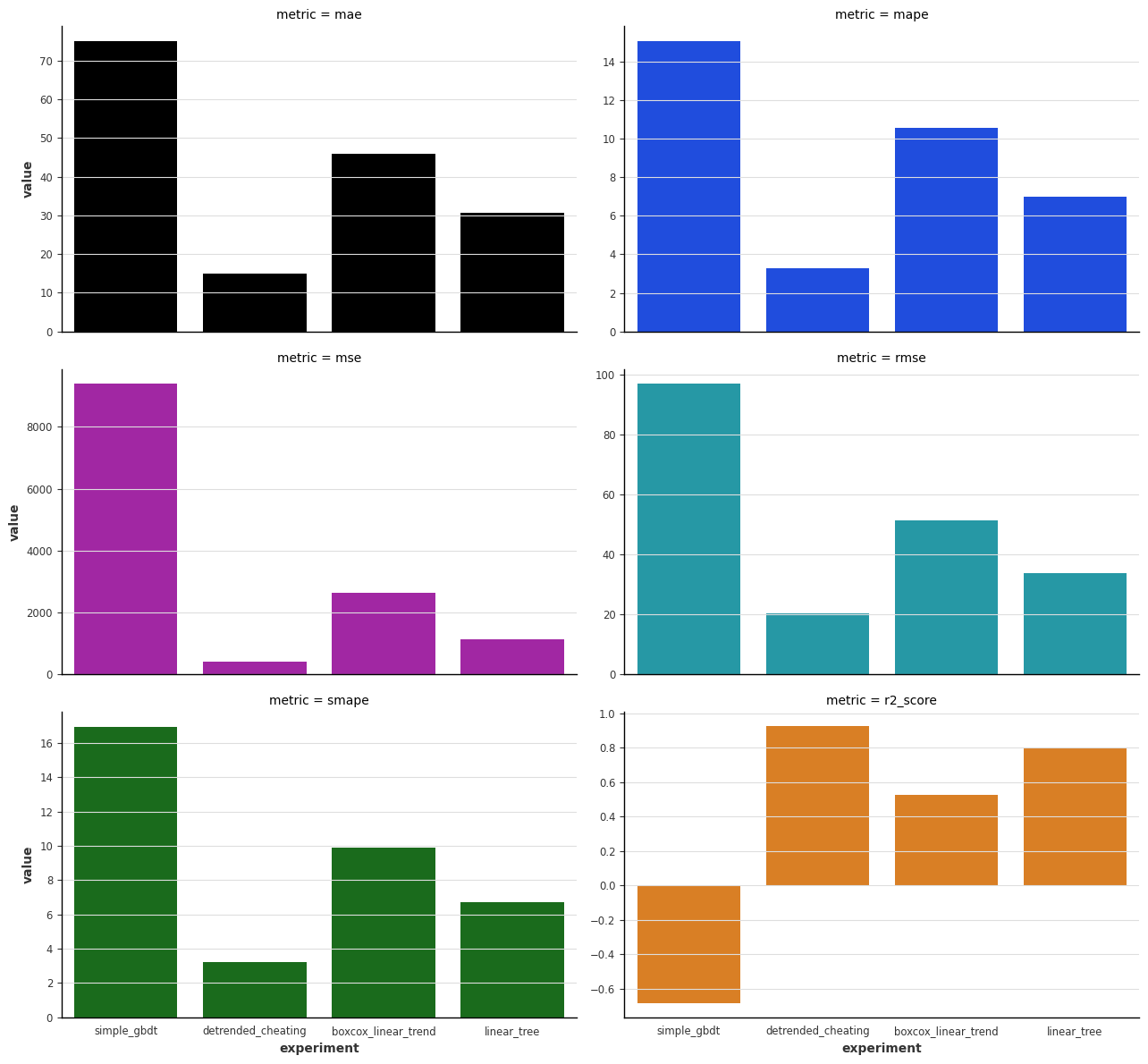
The benchmark metrics for the GBDT are shown below. As expected, linear tree and box-cox + linear trend models beat the baseline model.

Trees are Powerful

Up to this point, we may get the feeling that trees are not the best choices for forecasting. As a matter of fact, trees are widely used in many competitions and have achieved a lot in forecasting³. Apart from being simple and robust, trees can also be made probabilistic. Trees are also attractive as our first model to try because they usually already work quite well out of the box¹.

---

1. "Out of the box" sounds like something easy to do. However, if one ever reads the list of parameters of LightGBM, the thought of "easy" will immediately diminish. ↩

2. LightGBM. Parameters — LightGBM 4.3.0.99 documentation. In: LightGBM [Internet]. [cited 2 Feb 2024]. Available: https://lightgbm.readthedocs.io/en/latest/Parameters.html#linear_tree ↩↩

3. Januschowski T, Wang Y, Torkkola K, Erkkilä T, Hasson H, Gasthaus J. Forecasting with trees. International journal of forecasting 2022; 38: 1473–1481. ↩

---

Contributors: LM