KL Divergence¶
The Kullback–Leibler (KL) divergence is defined as
\[
\begin{align}
\operatorname{D}_\mathrm{KL}(p \parallel q ) =& \mathbb E_{p} \left[\log\left(\frac{p}{q}\right) \right] \\
=& \int_{-\infty}^\infty p \log\left(\frac{p}{q}\right)\, dx .
\end{align}
\]
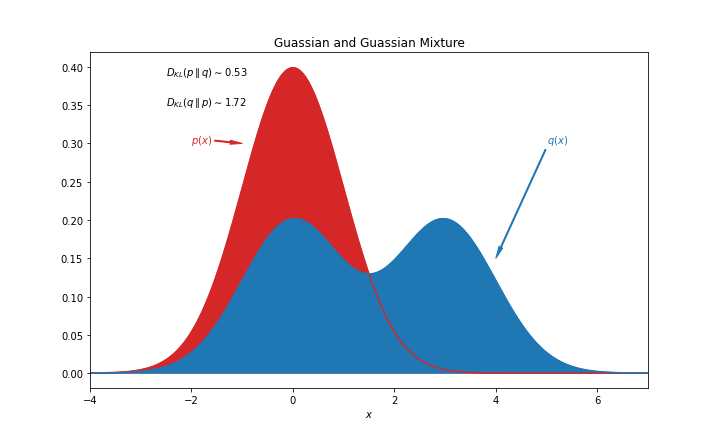
Suppose \(p\) is a Gaussian distribution and \(q\) is a bimodal Gaussian mixture, the KL divergence \(\operatorname{D}_\mathrm{KL}(p \parallel q )\) and \(\operatorname{D}_\mathrm{KL}(q \parallel p )\) are different as KL divergence is not necessarily symmetric. Thus the KL divergence is not a proper distance definition.
KL divergence is a special case of f-divergence.
Contributors: