Time Series Forecasting with Neural ODE¶
Jupyter Notebook Available
We have a 
notebook for this section which includes all the code used in this section.
Introduction to Neural ODE
We explain the theories of neuralode in this section. Please read it first if you are not familiar with neural ode.
In the section Neural ODE, we have introduced the concept of neural ODE. In this section, we will show how to use neural ODE to do time series forecasting.
A Neural ODE Model¶
We built a single hidden layer neural network as the field,
graph TD
input["Input (100)"]
input_layer["Hidden Layer (100)"]
output_layer["Output Layer (100)"]
hidden_layer["Hidden Layer (256)"]
output["Output (1)"]
input --> input_layer
input_layer --> hidden_layer
hidden_layer --> output_layer
output_layer --> outputThe model is built using the package called torchdyn 1.
Packages
Apart from the torchdyn package we used here, there is another package called torchdiffeq 2 which is developed by the authors of neural ode.
Single Step Forecasts¶
We trained the model using a history length of 100 and only forecast one step (with a gap of 3 between the input and target). The result is shown below.
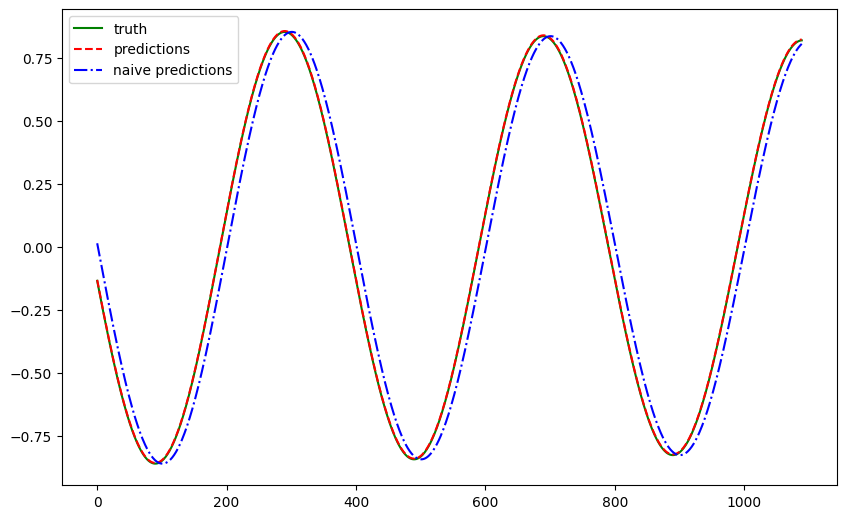
Neural ODE is a good forecaster for our pendulum dataset since the pendulum is simply generated by a differential equation. The metrics are also computed and listed below.
| Metric | Neural ODE | Naive |
|---|---|---|
| Mean Absolute Error | 0.003052 | 0.092666 |
| Mean Squared Error | 0.000009 | 0.010553 |
| Symmetric Mean Absolute Percentage Error | 0.021231 | 0.376550 |
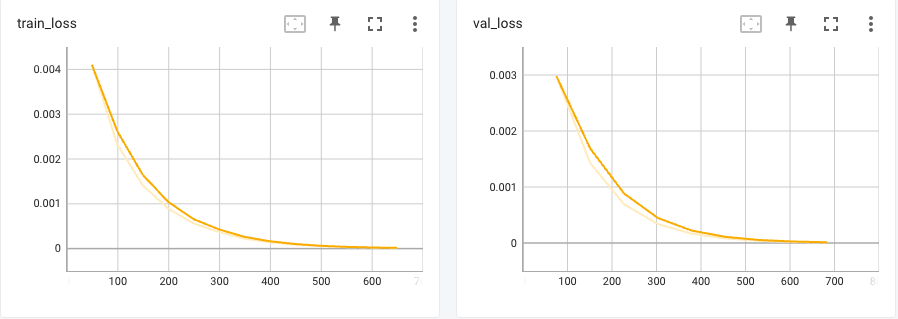
Training
The training loss is shown below.
Multi-Step Forecasts¶
We perform a similar experiment but forecast 3 steps.
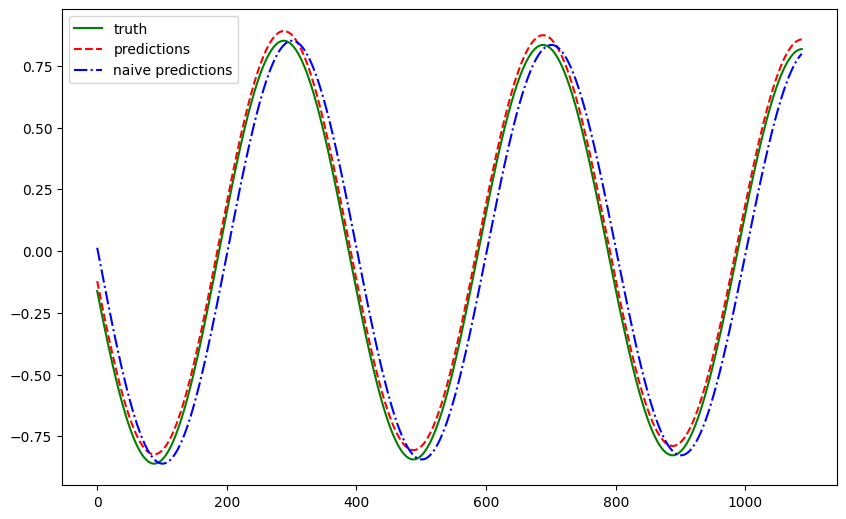
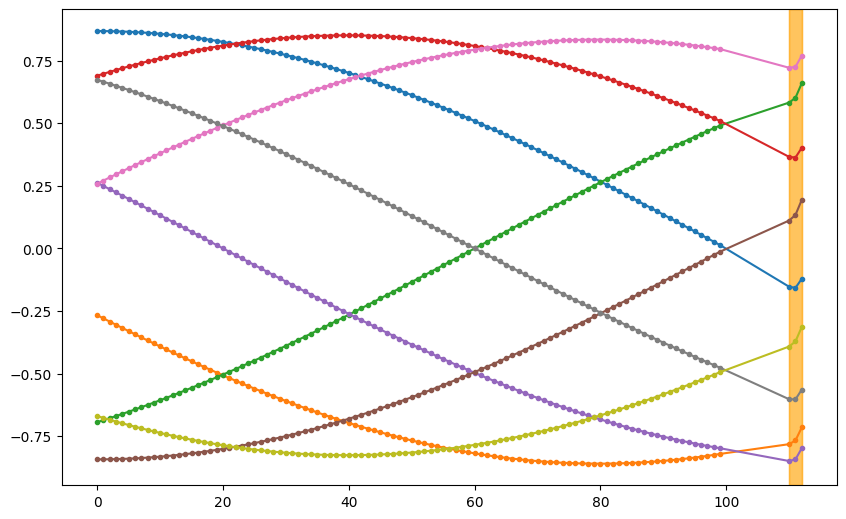
We plot out some samples and shade the predictions using orange color. The plot below shows that the forecasts are mostly on the right trend.
| Metric | Neural ODE | Naive |
|---|---|---|
| Mean Absolute Error | 0.038421 | 0.109485 |
| Mean Squared Error | 0.001478 | 0.014723 |
| Symmetric Mean Absolute Percentage Error | 0.153392 | 0.423563 |