Continuous Ranked Probability Score (CRPS)¶

The Continuous Ranked Probability Score, aka CRPS, is a score to measure how a proposed distribution approximates the data, without knowledge about the true distributions of the data.

Definition¶

CRPS is defined as¹

\[ \operatorname{CRPS}(P, x_a) = \int_{-\infty}^\infty \lVert P(x) - H(x - x_a) \rVert_2 dx, \]

where

$x_a$ is the true value of $x$,
P(x) is our proposed cumulative distribution for $x$,
$H(x)$ is the Heaviside step function,
$\lVert \cdot \rVert_2$ is the L2 norm.

Heaviside Step Function

\[ H(x) = \begin{cases} 1, &\qquad x=0\\ 0, &\qquad x\leq 0\\ \end{cases} \]

Explain it¶

The formula looks abstract on first sight, but it becomes crystal clear once we understand it.

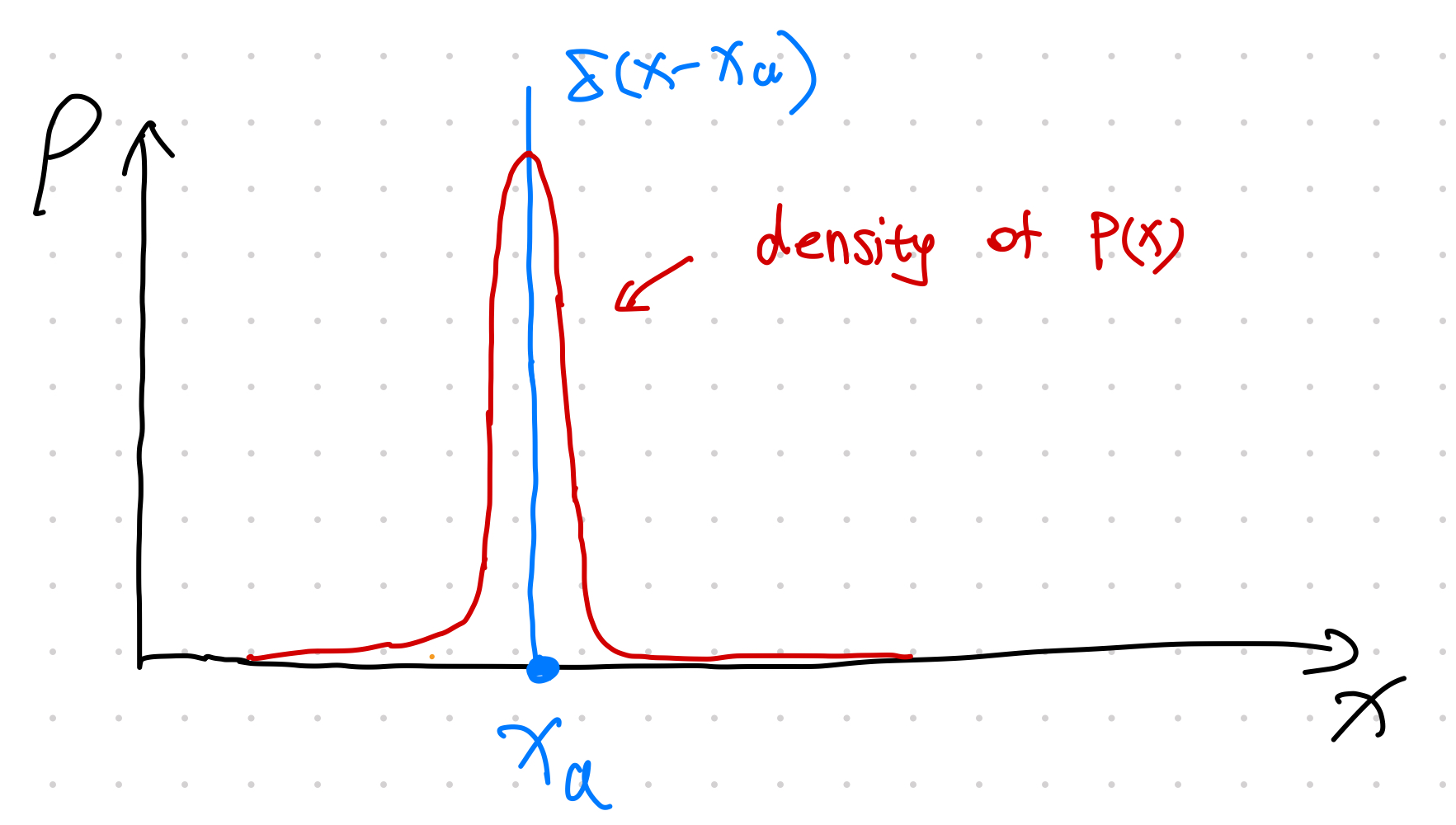
Note that the distribution that corresponds to a Heaviside CDF is the delta function $\delta(x-x_a)$. What this score is calculating is the difference between our distribution and a delta function. If we have a model that minimizes CRPS, then we are looking for a distribution that is close to the delta function $\delta(x-x_a)$. In other words, we want our distribution to be large around $x_a$.

To illustrate what the integrand $\lVert P(x) - H(x - x_a) \rVert_2$ means, we apply some shades to the integrand of the integral in CRPS. We visualize four difference scenarios.

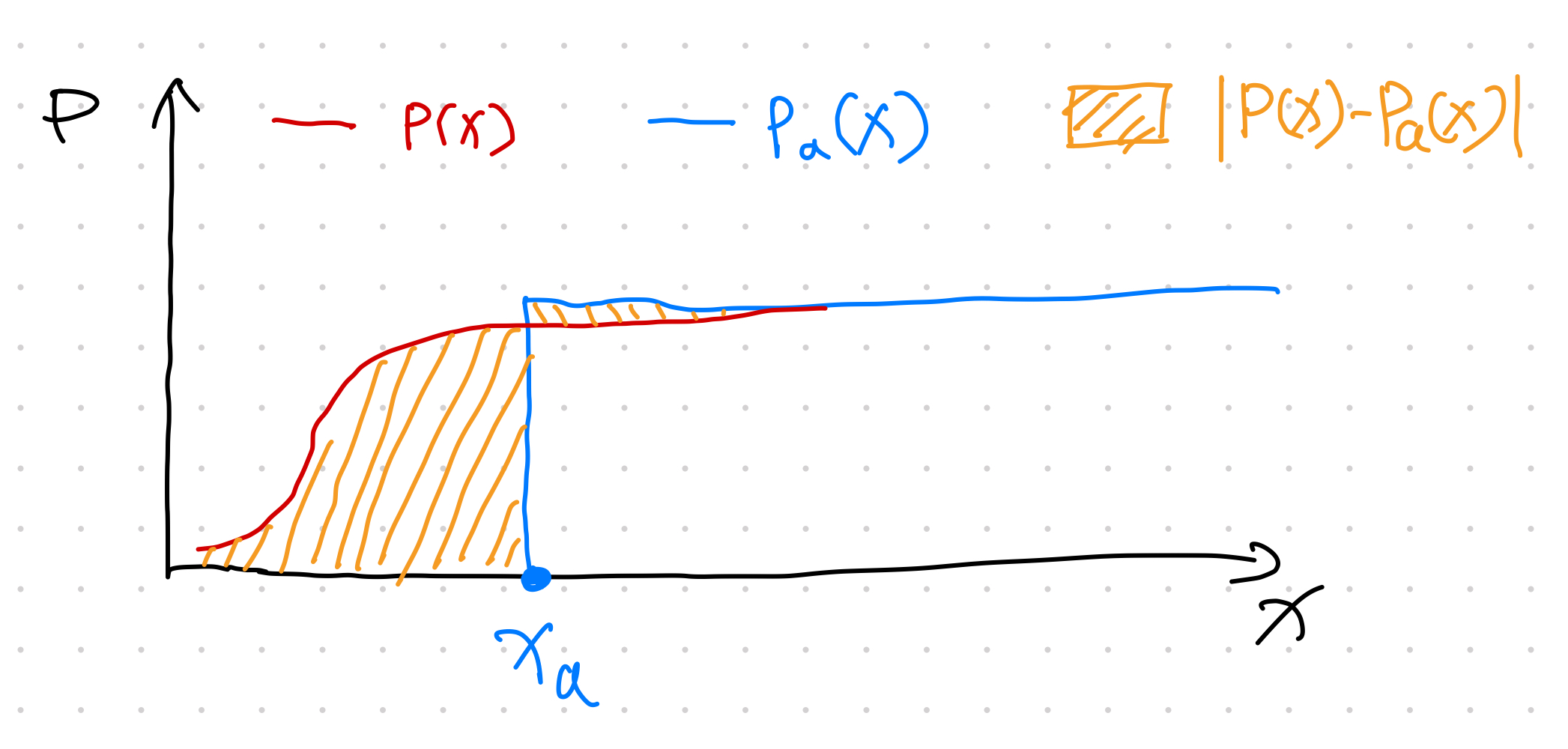
Scenario 1: The predicted CDF $P(x)$ is reaching 1 very fast.

$When the proposed CDF $P(x)$ is reaching 1 faster$

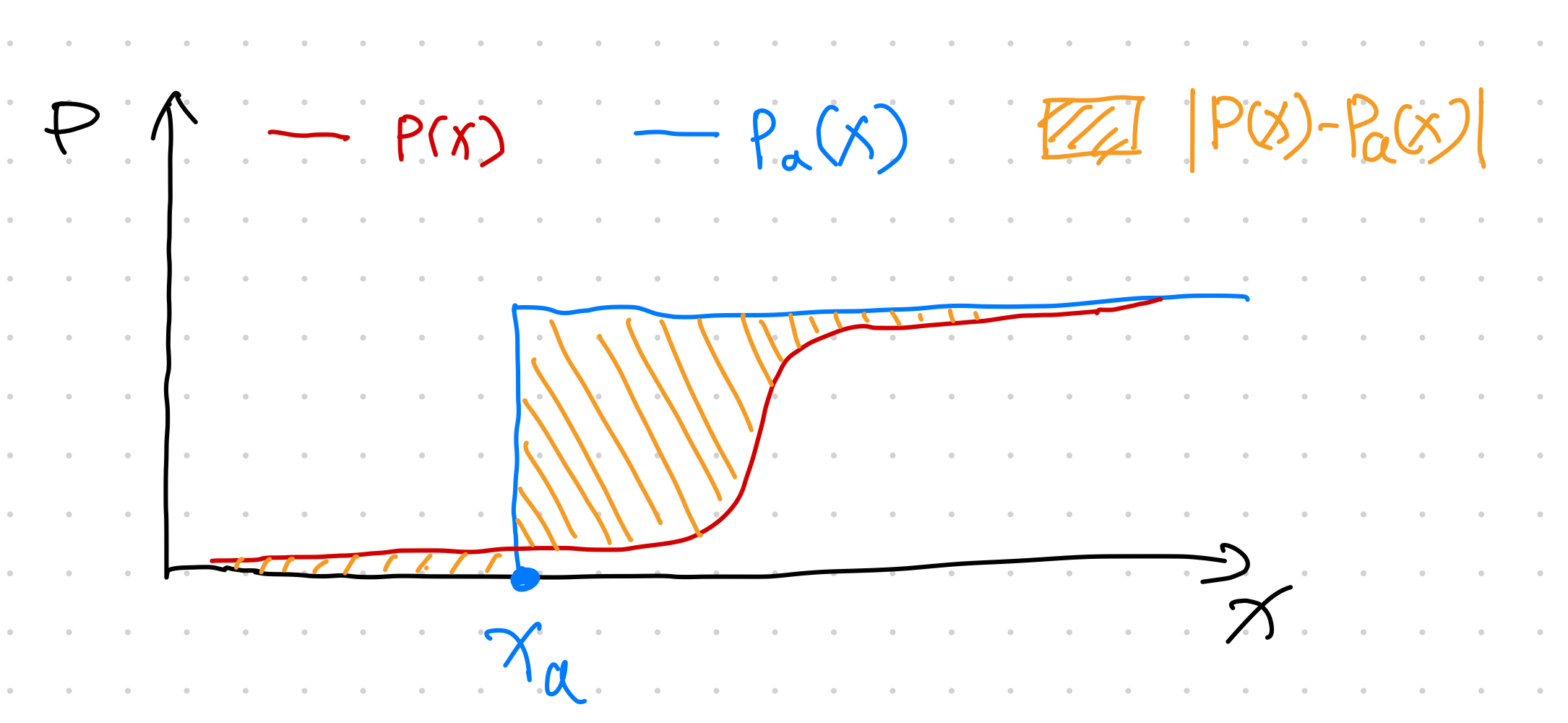
Scenario 2: The predicted CDF $P(x)$ is reaching 1 quite late.

$When the proposed CDF $P(x)$ is reaching 1 slower$

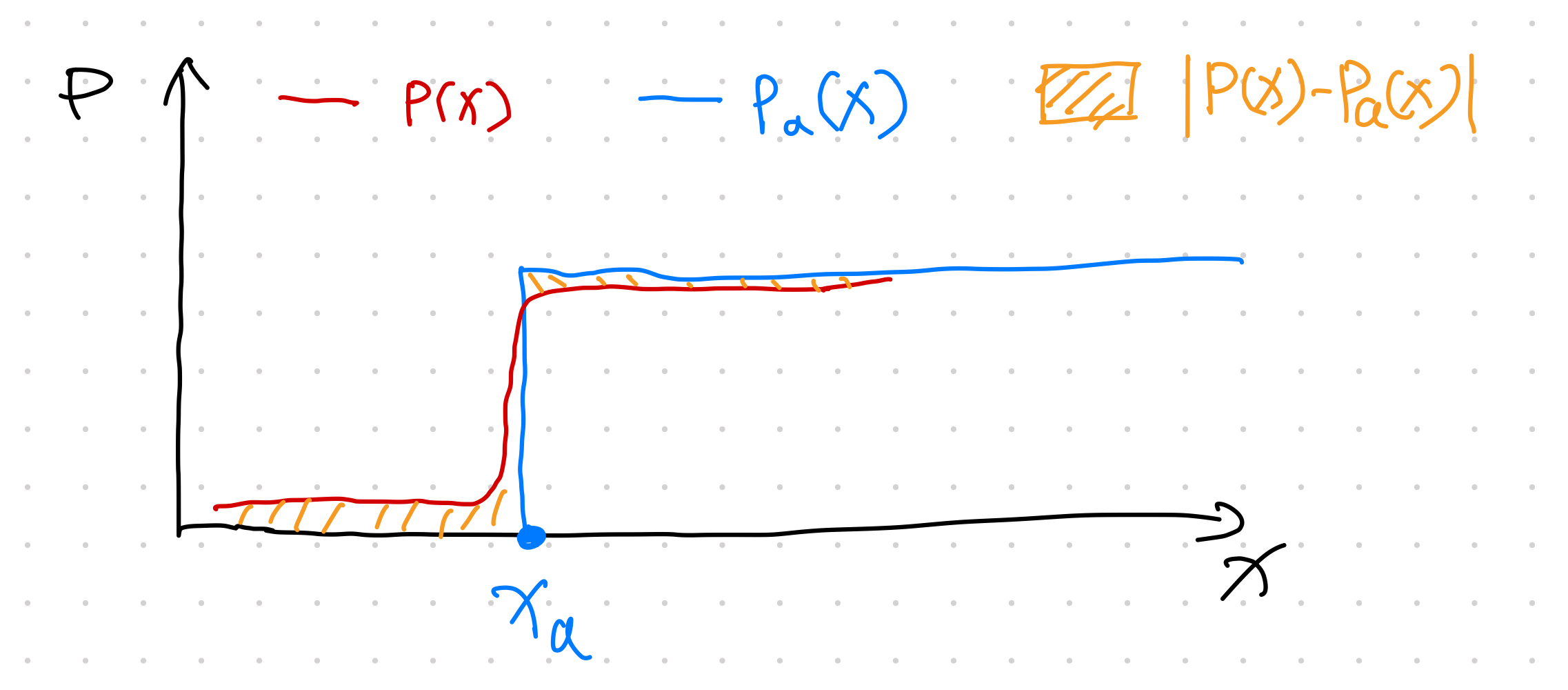
Scenario 3: The predicted CDF $P(x)$ is reaching 1 around the Heaviside function jump.

$When the proposed CDF $P(x)$ is close to the Heaviside function$

Scenario 4: The predicted CDF $P(x)$ is steadily increasing but very dispersed.

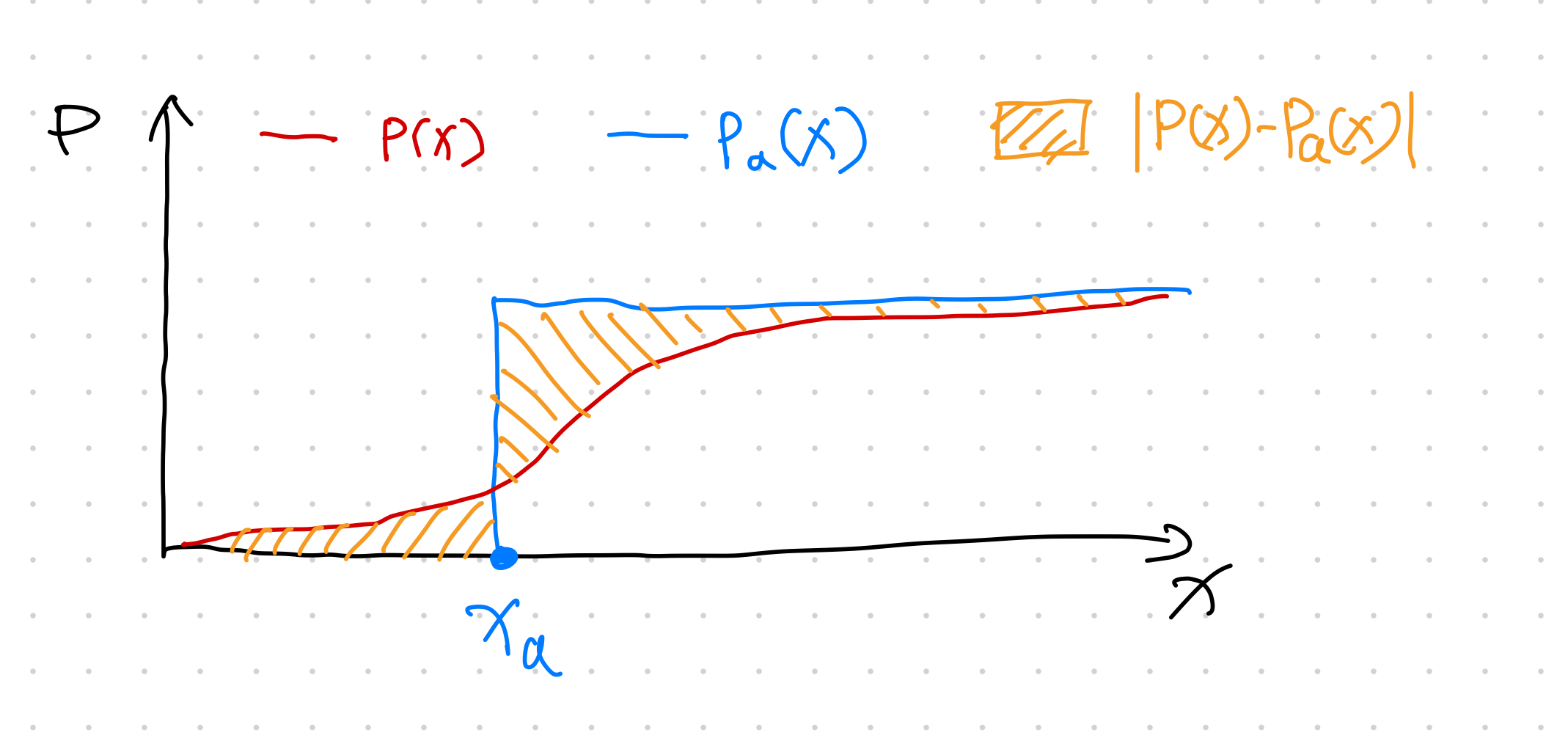
$When the proposed CDF $P(x)$ is dispersed around $x_a$$

With the four different scenarios visualized, intuitively, the only way to get a small CRPS score is to choose a distribution that is focused around $x_a$. Echoing a previous note on the delta function being the density function of the Heaviside function, we expect a small CRPS reflects a scenario of the following: the predicted distribution $\rho(x)$ is very focused around the observation $x_a$.

$densities of $P(x)$ and $H(x-x_a)$$

Discussions¶

Gebetsberger et al found that CRPS is more robust compared to Likelihood while producing similar results if we use a good assumption for the data distribution³.

CRPS is also very useful in time series forecasting. For example, the integrand of CRPS can be used as the loss function in model training ².

Contributors: LM