Flow¶
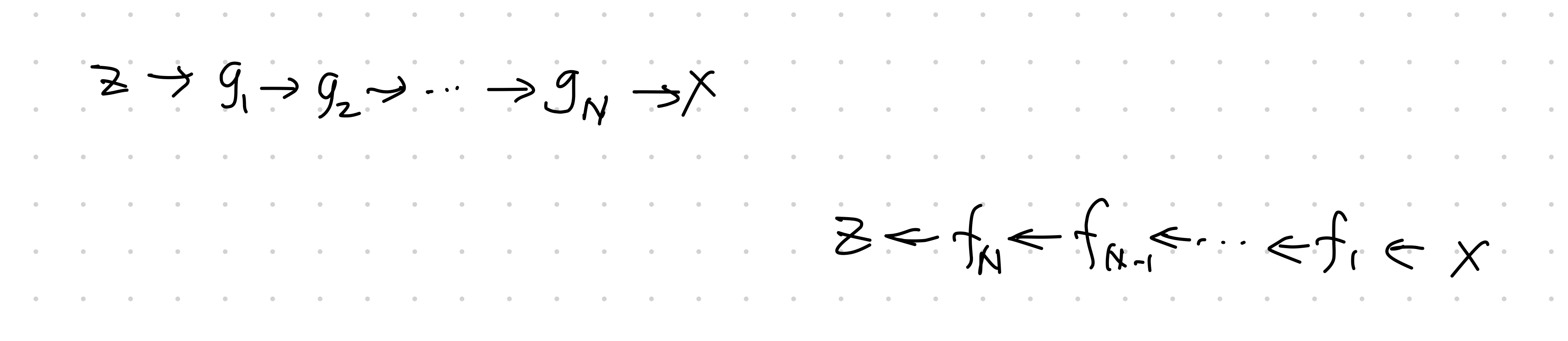
For a probability density \(p(x)\) and a transformation of coordinate \(x=g(z)\) or \(z=f(x)\), the density can be expressed using the coordinate transformations, i.e.,
\[
\begin{align}
p(x) &= \tilde p (f(x)) \lvert \operatorname{det} \operatorname{D} g(f(x)) \rvert^{-1} \\
&= \tilde p(f(x)) \lvert \operatorname{det}\operatorname{D} f(x) \rvert
\end{align}
\]
where the Jacobian is
\[
\operatorname{D} g(z) \to \frac{\partial }{\partial z} g.
\]
The operation \(g_{*}\circ \tilde p(z)\) is the push forward of \(\tilde p(z)\). The operation \(g_{*}\) will pushforward simple distribution \(\tilde p(z)\) to a more complex distribution \(p(x)\).
- The generative direction: sample \(z\) from distribution \(\tilde p(z)\), apply transformation \(g(z)\);
- The normalizing direction: "simplify" \(p(x)\) to some simple distribution \(\tilde p(z)\).
The key to the flow model is the chaining of the transformations
\[
\operatorname{det} \operatorname{D} f(x) = \Pi_{i=1}^N \operatorname{det} \operatorname{D} f_i (x_i)
\]
where
\[
\begin{align}
x_i &= g_i \circ \cdots \circ g_1 (z)\\
&= f_{i+1} \circ \cdots \circ f_N (x).
\end{align}
\]
-
Liu X, Zhang F, Hou Z, Wang Z, Mian L, Zhang J, et al. Self-supervised Learning: Generative or Contrastive. arXiv [cs.LG]. 2020. Available: http://arxiv.org/abs/2006.08218 ↩
Contributors: