Skip to content

Contrastive Predictive Coding

Contrastive Predictive Coding, CPC, is an autoregressive model combined with InfoNCE loss1.

Predictive Coding

As a related topic, predictive coding is a different scheme than backpropagation. Predictive coding updates the weights using local updating rules only2.

There are two key ideas in CPC:

  • Autoregressive models in latent space, and
  • InfoNCE loss that combines mutual information and NCE.

For the series of segments, \(\{x_t\}\), we apply an encoder on each segment, and calculate the latent space, \(\{{\color{blue}\hat x_t}\}\). The latent space \(\{{\color{blue}\hat x_t}\}\) is then modeled using an autoregressive model to calculate the coding, \(\{{\color{red}c_t}\}\).

van den Oord et al

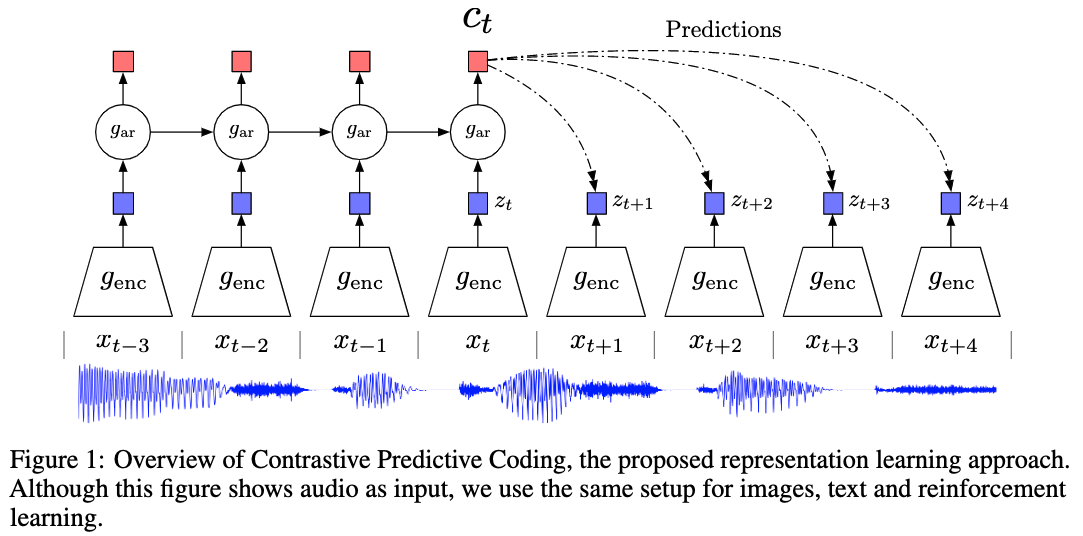
The loss is built on NCE to estimate the lower bound of mutual information,

\[ \mathcal L = -\mathbb E_X \left[ \log \frac{f_k(x_{t+k}, c_t)}{\sum_{j} f_k(x_{j}, c_t) } \right], \]

where \(f_k(x_{x+i}, c_t)\) is estimated using a log-bilinear model, \(f_k(x_{x+i}, c_t) = \exp\left( z_{t+i} W_i c_t \right)\). This is also a cross entropy loss.

Minimizing \(\mathcal L\) leads to a \(f_k\) that estimates the ratio1

\[ \frac{p(x_{t+k}\mid c_t)}{p(x_{t+k})} = \frac{p(x_{t+k}, c_t)}{p(x_{t+k})p(c_t)}. \]

We can perform downstream tasks such as classifications using the encoders.

Maximizing this lower bound?

This so-called lower bound for mutual information in this case is not always going to work[^Newell2020]. In some cases, the representations learned using this lower bound doesn't help or even worsen the performance of downstream tasks.

Code

rschwarz15/CPCV2-PyTorch

  1. van den Oord A, Li Y, Vinyals O. Representation learning with Contrastive Predictive Coding. arXiv [cs.LG]. 2018. Available: http://arxiv.org/abs/1807.03748 ↩↩

  2. Millidge B, Tschantz A, Buckley CL. Predictive coding approximates backprop along arbitrary computation graphs. 2020.http://arxiv.org/abs/2006.04182. ↩

Contributors: LM