InfoGAN¶
In GAN, the latent space input is usually random noise, e.g., Gaussian noise. The objective of GAN is a very generic one. It doesn't say anything about how exactly the latent space will be used. This is not desirable in many problems. We would like to have more interpretability in the latent space. InfoGAN introduced constraints to the objective to enforce interpretability of the latent space1.
Constraint¶
The constraint InfoGAN proposed is mutual information,
where
- \(c\) is the latent code,
- \(z\) is the random noise input,
- \(V({\color{green}D}, {\color{red}G})\) is the objective of GAN,
- \(I(c; {\color{red}G}(z,c))\) is the mutual information between the input latent code and generated data.
Using the lambda multiplier, we punish the model if the generator loses information in latent code \(c\).
Training¶
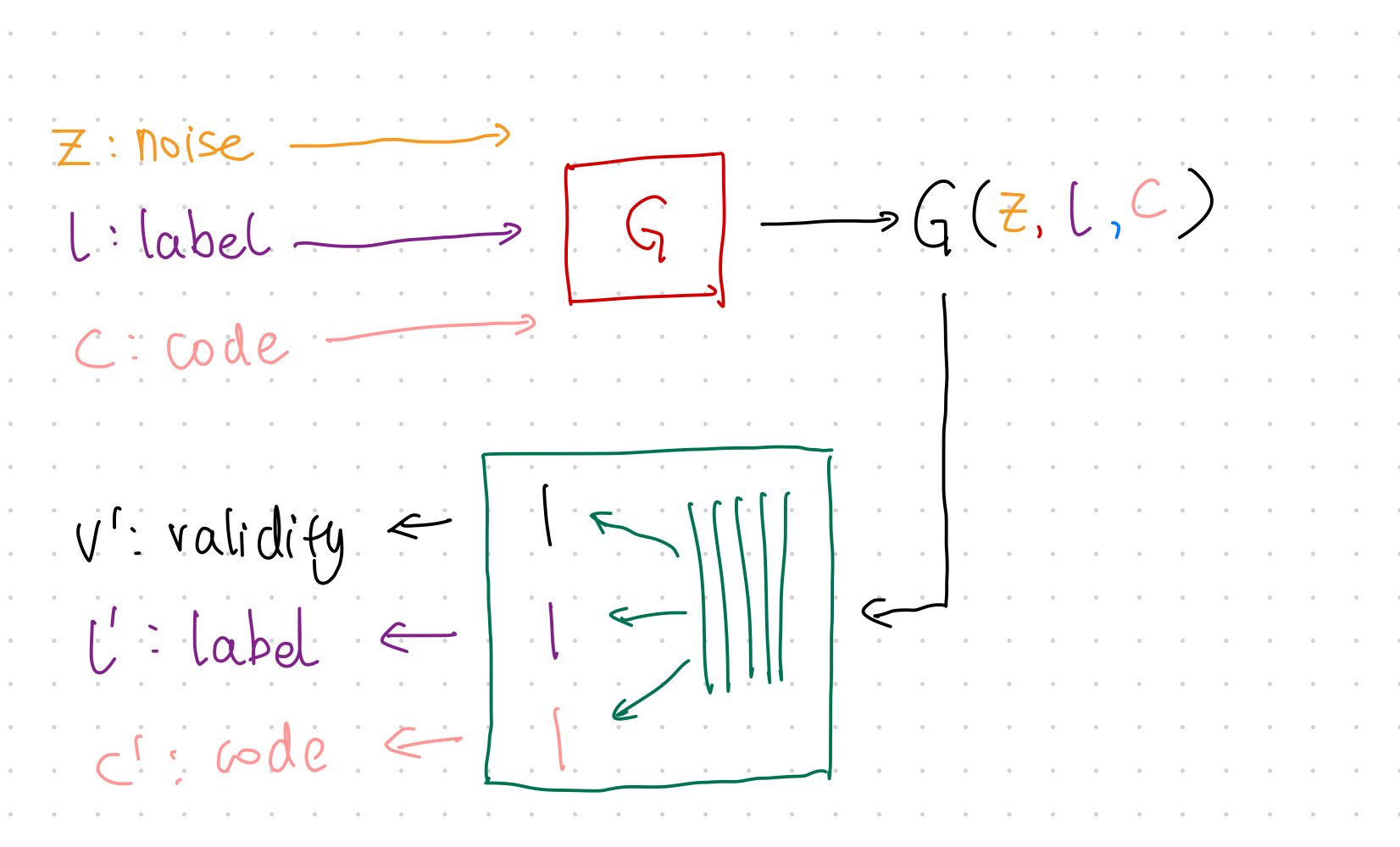
The training steps are almost the same as GAN but with one extra loss to be calculated in each mini-batch.
- Train \(\color{red}G\) using loss: \(\operatorname{MSE}(v', v)\);
- Train \(\color{green}D\) using loss: \(\operatorname{MSE}(v', v)\);
- Apply Constraint:
- Sample data from mini-batch;
- Calculate loss \(\lambda_{l} H(l';l)+\lambda_c \operatorname{MSE}(c,c')\)
Code¶
-
Chen X, Duan Y, Houthooft R, Schulman J, Sutskever I, Abbeel P. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. arXiv [cs.LG]. 2016. Available: http://arxiv.org/abs/1606.03657 ↩
-
Agakov DBF. The im algorithm: a variational approach to information maximization. Adv Neural Inf Process Syst. 2004. Available: https://books.google.com/books?hl=en&lr=&id=0F-9C7K8fQ8C&oi=fnd&pg=PA201&dq=Algorithm+variational+approach+Information+Maximization+Barber+Agakov&ots=TJGrkVS610&sig=yTKM2ZdcZQBTY4e5Vqk42ayUDxo ↩