VAR¶
VAR(1)¶
VAR(1) is similar to AR(1) but models time series with interactions between the series. For example, a two-dimensional VAR(1) model is
\[
\begin{pmatrix}s^{(1)}(t+1) \\ s^{(2)}(t+1) \end{pmatrix} = \begin{pmatrix} \phi^{(1)}_0 \\ \phi^{(2)}_0 \end{pmatrix} + \begin{pmatrix}\phi_{1, 11} & \phi_{1, 12}\\ \phi_{1, 21} & \phi_{1, 22} \end{pmatrix} \begin{pmatrix}s^{(1)}(t) \\ s^{(2)}(t) \end{pmatrix} + \begin{pmatrix}\epsilon^{(1)} \\ \epsilon^{(2)} \end{pmatrix}.
\]
A more compact form is
\[
\mathbf s (t+1) = \boldsymbol \phi_0 + \boldsymbol \phi_1 \mathbf s(t) + \boldsymbol \epsilon.
\]
Stability of VAR
For VAR(1), our series blows up when the max eigenvalue of the matrix \(\boldsymbol \phi_1\) is large than 11. Otherwise, we get stable series.
In the following examples, we denote the largest eigenvalue of \(\boldsymbol \phi_1\) as \(\lambda_0\).
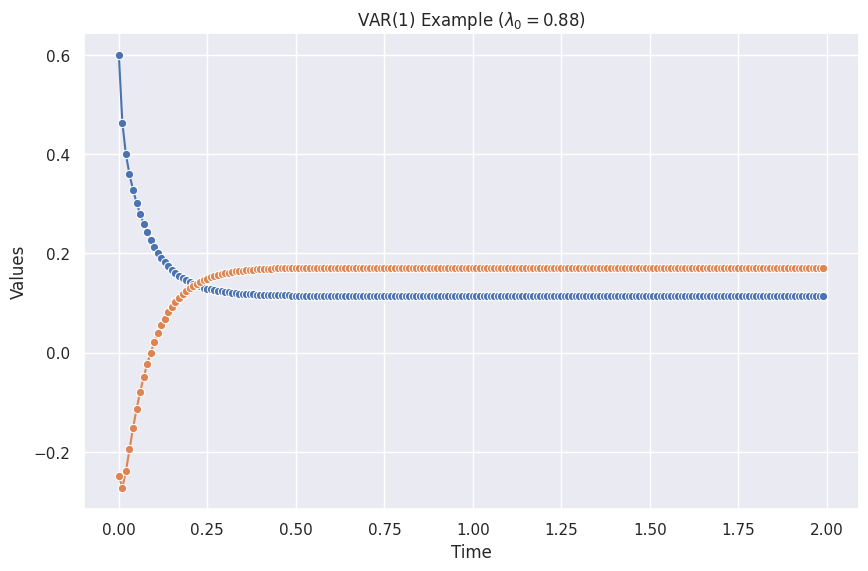
The figure is created using the code from the "Python Code" tab, and the following parameters.
var_params_stable = VAR1ModelParams(
delta_t = 0.01,
phi0 = np.array([0.1, 0.1]),
phi1 = np.array([
[0.5, -0.25],
[-0.35, 0.45+0.2]
]),
epsilon = ConstantEpsilon(epsilon=np.array([0,0])),
initial_state = np.array([1, 0])
)
var1_visualize(var_params=var_params_stable)
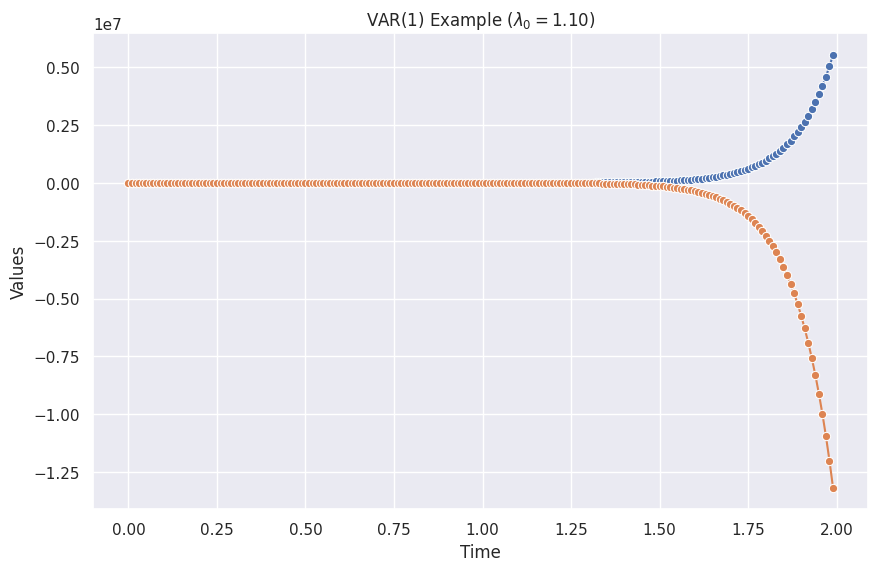
The figure is created using the code from the "Python Code" tab, and the following parameters.
var_params_unstable = VAR1ModelParams(
delta_t = 0.01,
phi0 = np.array([0.1, 0.1]),
phi1 = np.array([
[0.5, -0.25],
[-0.35, 0.45+0.5]
]),
epsilon = ConstantEpsilon(epsilon=np.array([0,0])),
initial_state = np.array([1, 0])
)
var1_visualize(var_params=var_params_unstable)
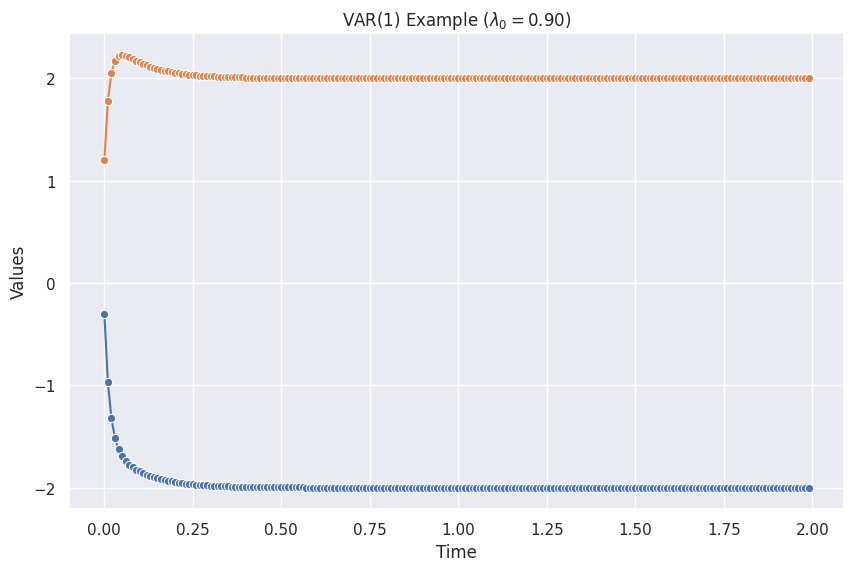
The figure is created using the code from the "Python Code" tab, and the following parameters.
var_params_no_noise = VAR1ModelParams(
delta_t = 0.01,
phi0 = np.array([-1, 1]),
phi1 = np.array([
[0.7, 0.2],
[0.2, 0.7]
]),
epsilon = ConstantEpsilon(epsilon=np.array([0,0])),
initial_state = np.array([1, 0])
)
var1_visualize(var_params=var_params_no_noise)
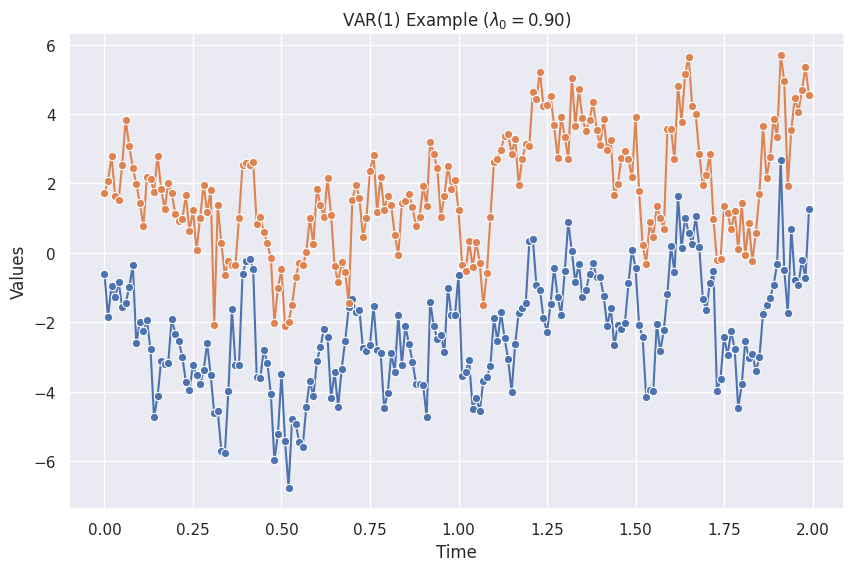
The figure is created using the code from the "Python Code" tab, and the following parameters.
var_params_zero_mean_noise = VAR1ModelParams(
delta_t = 0.01,
phi0 = np.array([-1, 1]),
phi1 = np.array([
[0.7, 0.2],
[0.2, 0.7]
]),
epsilon = MultiGaussianNoise(mu=np.array([0, 0]), cov=np.array([[1, 0.5],[0.5, 1]])),
initial_state = np.array([1, 0])
)
var1_visualize(var_params=var_params_zero_mean_noise)
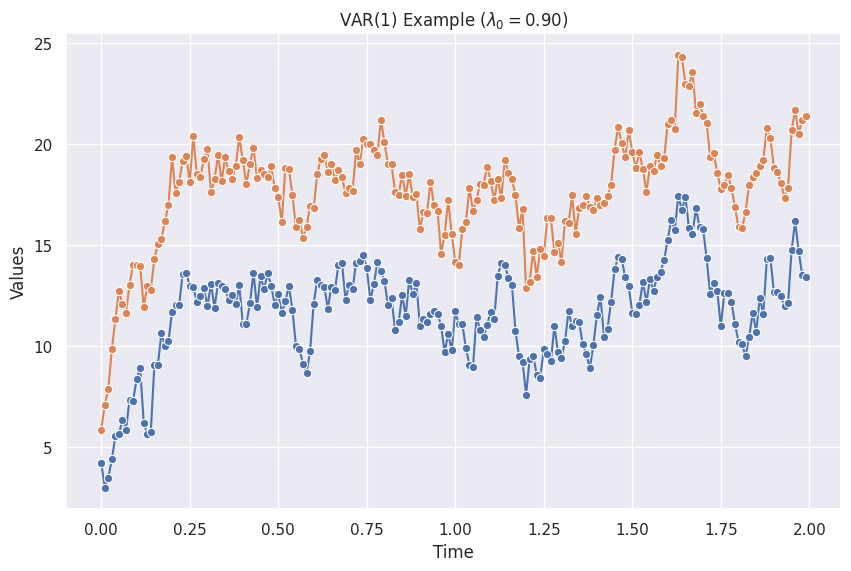
The figure is created using the code from the "Python Code" tab, and the following parameters.
var_params_nonzero_mean_noise = VAR1ModelParams(
delta_t = 0.01,
phi0 = np.array([-1, 1]),
phi1 = np.array([
[0.7, 0.2],
[0.2, 0.7]
]),
epsilon = MultiGaussianNoise(mu=np.array([1, 2]), cov=np.array([[1, 0.5],[0.5, 1]])),
initial_state = np.array([1, 0])
)
var1_visualize(var_params=var_params_nonzero_mean_noise)
import copy
from dataclasses import dataclass
from typing import Iterator
import numpy as np
class MultiGaussianNoise:
"""A multivariate Gaussian noise
:param mu: means of the variables
:param cov: covariance of the variables
:param seed: seed of the random number generator for reproducibility
"""
def __init__(self, mu: np.ndarray, cov: np.ndarray, seed: Optional[float] = None):
self.mu = mu
self.cov = cov
self.rng = np.random.default_rng(seed=seed)
def __next__(self) -> np.ndarray:
return self.rng.multivariate_normal(self.mu, self.cov)
class ConstantEpsilon:
"""Constant noise
:param epsilon: the constant value to be returned
"""
def __init__(self, epsilon=0):
self.epsilon = epsilon
def __next__(self):
return self.epsilon
@dataclass(frozen=True)
class VAR1ModelParams:
"""Parameters of our VAR model,
:param delta_t: step size of time in each iteration
:param phi0: pho_0 in the AR model
:param phi1: pho_1 in the AR model
:param epsilon: noise iterator, e.g., Gaussian noise
:param initial_state: a dictionary of the initial state, e.g., `{"s": 1}`
"""
delta_t: float
phi0: np.ndarray
phi1: np.ndarray
epsilon: Iterator
initial_state: np.ndarray
class VAR1Stepper:
"""Calculate the next values using VAR(1) model.
:param model_params: the parameters of the VAR(1) model, e.g.,
[`VAR1ModelParams`][eerily.data.generators.var.VAR1ModelParams]
"""
def __init__(self, model_params):
self.model_params = model_params
self.current_state = copy.deepcopy(self.model_params.initial_state)
def __iter__(self):
return self
def __next__(self):
epsilon = next(self.model_params.epsilon)
phi0 = self.model_params.phi0
phi1 = self.model_params.phi1
self.current_state = phi0 + np.matmul(phi1, self.current_state) + epsilon
return copy.deepcopy(self.current_state)
class Factory:
"""A generator that creates the data points based on the stepper."""
def __init__(self):
pass
def __call__(self, stepper, length):
i = 0
while i < length:
yield next(stepper)
i += 1
We create a function to visualize the series.
def var1_visualize(var_params):
phi1_eig_max = max(np.linalg.eig(var_params.phi1)[0])
var1_stepper = VAR1Stepper(model_params=var_params)
length = 200
fact = Factory()
history = list(fact(var1_stepper, length=length))
df = pd.DataFrame(history, columns=["s1", "s2"])
print(df.head())
fig, ax = plt.subplots(figsize=(10, 6.18))
sns.lineplot(
x=np.linspace(0, length-1, length) * var_params.delta_t,
y=df.s1,
ax=ax,
marker="o",
)
sns.lineplot(
x=np.linspace(0, length-1, length) * var_params.delta_t,
y=df.s2,
ax=ax,
marker="o",
)
ax.set_title(f"VAR(1) Example ($\lambda_0={phi1_eig_max:0.2f}$)")
ax.set_xlabel("Time")
ax.set_ylabel("Values")
-
Zivot E, Wang J. Modeling Financial Time Series with S-PLUS®. Springer New York; 2006. doi:10.1007/978-0-387-32348-0 ↩
Contributors: