Transformers for Time Series Forecasting

Jupyter Notebook Available

We have a notebook for this section which includes all the code used in this section.

Introduction to Transformers

We explain the theories of transformers in this section. Please read it first if you are not familiar with transformers.

Transformer is a good candidate for time series forecasting due to its sequence modeling capability¹². In this section, we will introduce some basic ideas of transformer-based models for time series forecasting.

Transformer for Univariate Time Series Forecasting

We take a simple Univariate time series forecasting task as an example. There are implementations of transformers for multivariate time series forecasting with all sorts of covariates, but we focus on univariate forecasting problem for simplicity.

Dataset

In this example, we use the pendulumn physics dataset.

Model

We built a naive transformer that only has an encoder. The input is passed to a linear layer to convert the tensor to the shape accepted by the encoder. The tensor is then passed to the encoder. The output of the encoder is passed to another linear layer to convert the tensor to the shape of the output.

flowchart TD

input_linear_layer[Linear Layer for Input]
positional_encoder[Positional Encoder]
encoder[Encoder]
output_linear_layer[Linear Layer for Output]

input_linear_layer --> positional_encoder
positional_encoder --> encoder
encoder --> output_linear_layer

Decoder is Good for Covariates

A decoder in a transformer model is good for capturing future covariates. In our problem, we do not have any covariates at all.

Positional Encoder

In this experiment, we do not include positional encoder as it introduces more complexities but it doesn't help that much in our case³.

Evaluations

Training

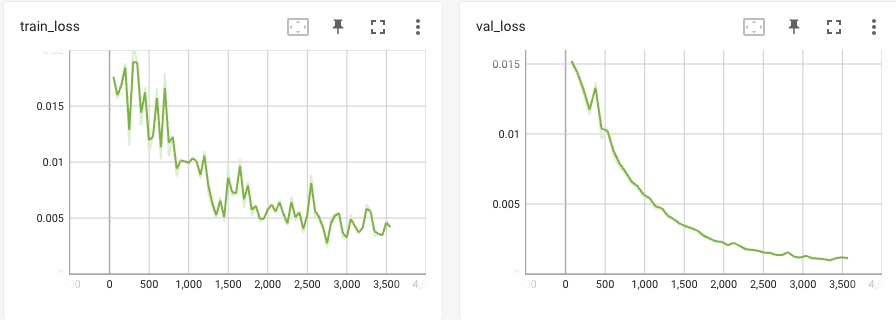
The details for model training can be found in this notebook. We will skip the details but show the loss curve here.

We trained the model using a history length of 50 and plotted the forecasts for a test dataset that was held out from training. The forecasts are plotted in red and the ground truth is plotted in blue.

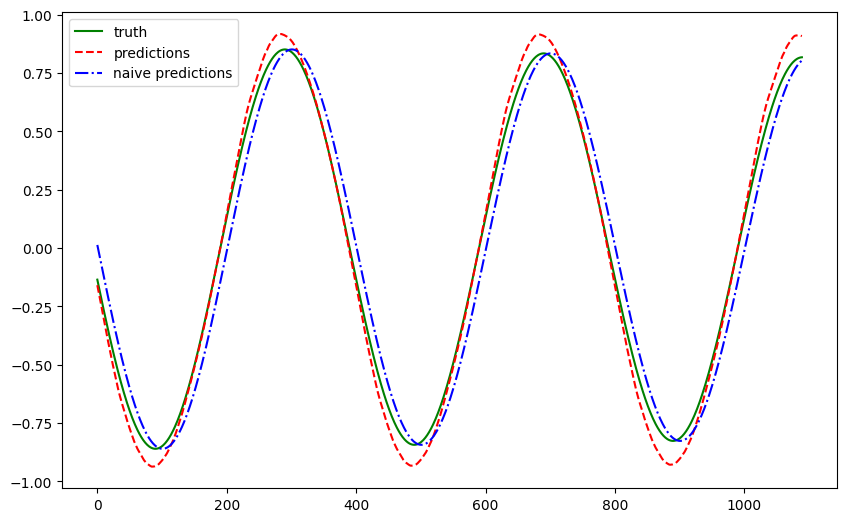
The forecasts roughly captured the patterns of the pendulum. To quantify the results, we compute a few metrics.

Metric	Vanilla Transformer	Naive
Mean Absolute Error	0.050232	0.092666
Mean Squared Error	0.003625	0.010553
Symmetric Mean Absolute Percentage Error	0.108245	0.376550

Multi-horizon Forecasting

We perform a similar experiment for multi-horizon forecasting (horizon=3). We plot out some samples. In the plot, the orange-shaded regions are the predictions.

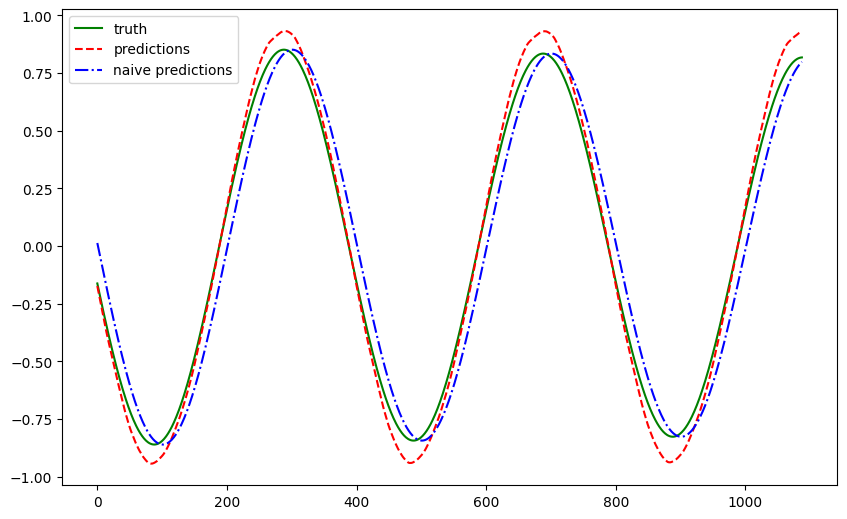
To verify that the forecasts make sense, we also plot out a few samples.

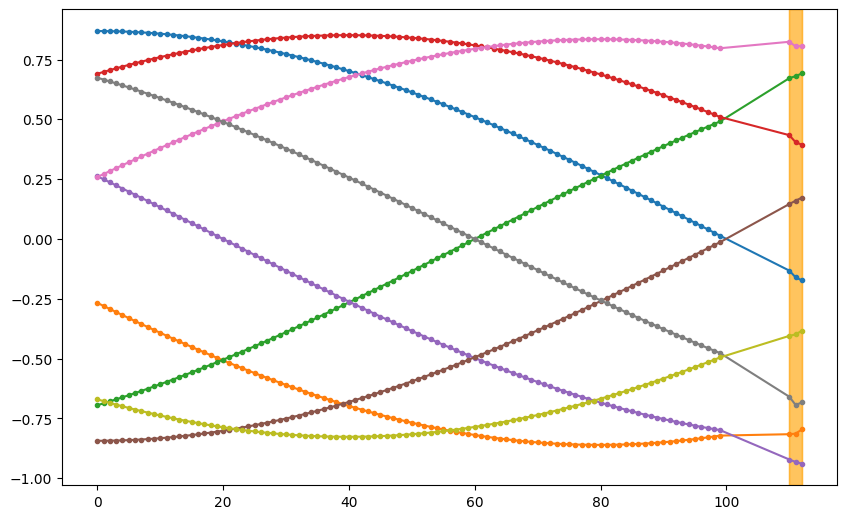
The following is a table of the metrics.

Metric	Vanilla Transformer	Naive
Mean Absolute Error	0.057219	0.109485
Mean Squared Error	0.004241	0.014723
Symmetric Mean Absolute Percentage Error	0.112247	0.423563

Generalization

The vanilla transformer has its limitations. For example, it doesn't capture the correlations between the series that well. There are many variants of transformers that are designed just for time series forecasting⁴⁵⁶⁷⁸⁹.

A few forecasting packages implemented transformers for time series forecasting. For example, the neuralforecast package by Nixtla has implemented TFT, Informer, AutoFormer, FEDFormer, and PatchTST, as of November 2023. An alternative is darts. These packages provide documentation and we encourage the reader to check them out for more complicated use cases of transformer-based models.

---

1. Ahmed S, Nielsen IE, Tripathi A, Siddiqui S, Rasool G, Ramachandran RP. Transformers in time-series analysis: A tutorial. 2022. doi:10.1007/s00034-023-02454-8. ↩

2. Wen Q, Zhou T, Zhang C, Chen W, Ma Z, Yan J et al. Transformers in time series: A survey. 2022.http://arxiv.org/abs/2202.07125. ↩

3. Zhang Y, Jiang Q, Li S, Jin X, Ma X, Yan X. You may not need order in time series forecasting. arXiv [csLG] 2019.http://arxiv.org/abs/1910.09620. ↩

4. Lim B, Arik SO, Loeff N, Pfister T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. 2019.http://arxiv.org/abs/1912.09363. ↩

5. Wu H, Xu J, Wang J, Long M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. 2021.https://github.com/thuml/Autoformer. ↩

6. Zhou H, Zhang S, Peng J, Zhang S, Li J, Xiong H et al. Informer: Beyond efficient transformer for long sequence time-series forecasting. 2020.http://arxiv.org/abs/2012.07436. ↩

7. Nie Y, Nguyen NH, Sinthong P, Kalagnanam J. A time series is worth 64 words: Long-term forecasting with transformers. 2022.http://arxiv.org/abs/2211.14730. ↩

8. Zhou T, Ma Z, Wen Q, Wang X, Sun L, Jin R. FEDformer: Frequency enhanced decomposed transformer for long-term series forecasting. 2022.http://arxiv.org/abs/2201.12740. ↩

9. Liu Y, Hu T, Zhang H, Wu H, Wang S, Ma L et al. ITransformer: Inverted transformers are effective for time series forecasting. 2023.http://arxiv.org/abs/2310.06625. ↩

---

Contributors: LM